top of page

ANALYZING QUADRATICS

 

Quadratics is a complex unit, but once you know the basics, it will be much easier to understand the concepts. 



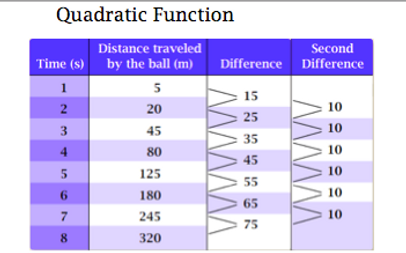
Second Differance

The second differance is what diffrenciates if the equation/realtion is quadratic or not. In linear systems, the first differance of the equations are the same; however if the equation is quadratic then it will have unequal first differnces. Quadratic realationships will have the same second differance.

 

The Parabola

 

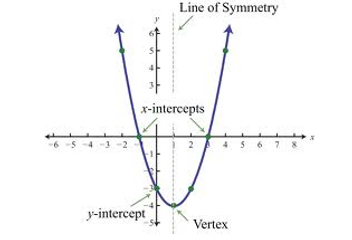
When a quadratic relation is graphed, It forms a type of curve known as the parabola.

Parabolas consist of features such as: 

Vertex : where the axis of symmetry and parabola meet

The axis of symmetry : Divides the parabola into two equal halves

Optimal value : the y co-ordinate of the vertex/ highest or lowest point

X- intercepts : the zeroes/ all real numbers

Y- intercept : The point where the graph crosses the y-axis

Learn More:

Factored Form



I'm a paragraph. Click here to add your own text and edit me. Let your users get to know you.
​
July 12, 2023​

Word Problems



Why quadractics? Go to word problems to find out the significance of how we use this in our life.
​
July 12, 2023​

Reflections



Check out the unit reflections to find out about what Dilpreet thinks about quadratics!
​
July 12, 2023​

Transformations



When an equation is in vertex form each letter is responsible for a transformation.

Transformations:

  • The (-h) moves the vertex of the parabola left or right *When the h is negative move right and when its positive move left

  • The (k) moves the vertex of the parabola up or down

        *When the k is negative move down and move up when its              positive

  • The (a) stretches the parabola and if the  (a) is a negative the parabola opens down 

        *It multiplies the vertical part of the step pattern

Vertex= (h,k)

 

Once the vertex of a parabola is indicated the basic step pattern is used to find the rest of the points.

bottom of page