top of page

Standard Form

ax²+bx+c

Solving using the quadratic equation

The quadratic equation is a formula which is used to find the x-intercepts. This equation can substitute factoring; and is recommended to use if the equation is not easily factor-able.

Example:

Solve the follwoing:

2x²−5x-6=0

 

STEP1: Find coefficients a , b and c.

a=2     b=-5     c=-6

 

STEP2: Plug in the values for a, b, and c into the quadratic formula

 

STEP3: Simplify expression under the square root.

 

STEP4: Solve for x

x= (3.4,0) OR x=(-0.9,0)

 

 

*If you want to check your answer, just plug in the x value into the equation and make sure it equals to 0.

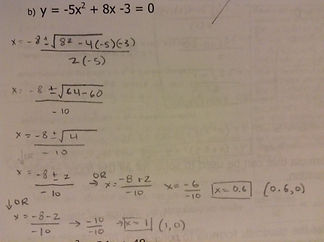
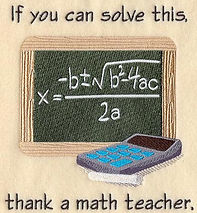
The Discriminant

Since the quadratic formula has been introduced, it is time to learn about one of the important parts in the formula. This part is known as the discriminant.

 

The b²-4ac part of the equation is the discrimiant.

 

The discriminant helps to determine how many solutions the equation has.

 

For instance:

When b²-4ac=a postive outcome:

there will be 2 real roots.

 

When b²-4ac=0:

there will be 1 double root.

 

When b²-4ac= a negative outcome:

there will be no real roots

 

 

Completing the Square

start with:  x²+6x+7

 ("b" is 6 in this case) 

   

1. Complete the Square:

Do this by dividing 6 by        

2 and square it (3)². The result is                                                           

9. Then add 9 and subtract 9

from x²+6x. We have to subtract                                                      2. Subtract the new term

because you cant add anything to the equation, but when you add and subtract it is like adding nothing.

3. Simplify it and we are done.

  

 

 

 

 

4. The result:                             x² + 6x + 7   =   (x+3)² âˆ’ 2  --> this answer is in vertex form a(x-h)²+k

 

IMPORTANT TIP:

If the a value of the equation is greater than 1, then you have to multiply the a value with the number taken out of the braket. For example:

Say you had the equation 3x²+6x+7

=3x²(6x+9-9)²+7

 

You have to multiply -9 by 3 before taking it out of the braket.

=3x²(6x+9)²+7-27

The result of the k value is now -20.

 

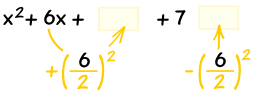
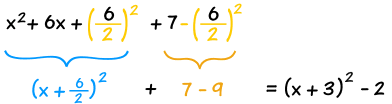
Graphing Standard Form

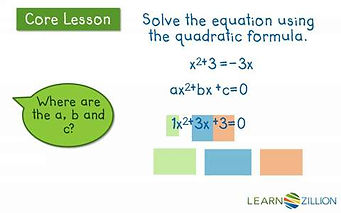
Here is an extra video about graphing standard form:

 

bottom of page